How The Boost Converters Work
Contributed By Imran Ashraf Khan
A boost converter (also called step-up converter) is a DC to DC converter circuit which is designed to convert an input DC voltage into an output DC voltage with a level that may be much higher than the input voltage level.
However the process always conserves the relation P = I x V, which means that as the output of the converter steps up the input voltage, the output proportionately undergoes a reduction in current, which causes the output power to be almost always equal to the input power or less than the input power.
How a Boost Converter Works
A boost converter is a kind of SMPS or switch mode power supply which fundamentally works with two active semiconductors (transistor and diode) and with a minimum of one passive component in the form of a capacitor or an inductor or both for greater efficiency.
The inductor here basically is used for stepping up the voltage and the capacitor is introduced for filtering the switching fluctuations and for reducing current ripples at the output of the converter.
The input power supply which may be required to be boosted or stepped up could be acquired from any suitable DC source such as batteries, solar panels, motor based generators etc.
Operating Principle
The inductor in a boost converter plays the important of stepping up the input voltage.
The crucial aspect which becomes responsible for activating the boost voltage from an inductor is due to its inherent property of resisting or opposing a suddenly induced current across it, and due to its response to this with a creation of magnetic field and subsequently destroying of the magnetic field. The destroying leads to the releasing of the stored energy.
This above process results in the storing of the current in the inductor and kicking back this stored current across the output in the form of back EMF.
A relay transistor driver circuit can be considered a great example of a boost converter circuit. The flyback diode connected across the relay is introduced to short circuit the reverse back EMFs from the relay coil and to protect the transistor whenever it switches OFF.
If this diode is removed and a diode capacitor rectifier is connected across the transistor's collector/emitter, the boosted voltage from the relay coil can be collected across this capacitor.
The process in a boost converter design results in an output voltage that’s always higher than the input voltage.
Referring to the following figure, we can see a standard boost converter configuration, the working pattern may be understood as given under:
When the shown device (which could be any standard power BJT or a mosfet) is switched ON, current from the input supply enters the inductor and flows clockwise through the transistor to complete the cycle at the negative end of the input supply.
During the above process the inductor experiences a sudden introduction of current across itself and tries to resist the influx, which results in the storing of some amount of the current in it through the generation of a magnetic field.
At the next subsequent sequence, when the transistor is switched OFF, the conduction of current breaks, yet again forcing a sudden change in the current level across the inductor. The inductor responds to this by kicking back or releasing the stored current. Since the transistor is in the OFF position, this energy finds its path through the diode D and across the shown output terminals in the form of a back EMF voltage.
The inductor performs this by destroying the magnetic field which was earlier created in it while the transistor was in the switch ON mode.
However, the above process of releasing energy is implemented with an opposite polarity, such that the input supply voltage now becomes in series with the inductor back emf voltage. And as we all know that when supply sources join in series their net voltage adds up to produce a bigger combined outcome.
The same happens in a boost converter during the inductor discharge mode, producing an output which may be the combined result of the inductor back EMF voltage and the existing supply voltage, as shown the diagram above
This combined voltage results in a boosted output or a stepped up output which finds its path through the diode D and the across capacitor C to ultimately reach the connected load.
The capacitor C plays quite an important role here, during the inductor discharge mode the capacitor C stores the released combined energy in it, and during the next phase when the transistor switches OFF again and the inductor is in the storing mode, the capacitor C tries to maintain the equilibrium by supplying its own stored energy to the load. See the figure below.
This ensures a relatively steady voltage for the connected load which is able to acquire power during both the ON, and OFF periods of the transistor.
If C is not included then this feature is cancelled resulting in a lower power for the load and lower efficiency rate.
The above explained process continues as the transistor is switched ON/OFF at a given frequency, sustaining the boost conversion effect.
Modes of Operation
A boost converter may be primarily operated in two modes: the continuous mode, and the discontinuous mode.
In continuous mode, the inductor current is never allowed to reach zero during its discharging process (while the transistor is switched OFF).
This happens when the ON/OFF time of the transistor is dimensioned in such a way that the inductor is always connected back quickly with the input supply through the switched ON transistor, before it’s able to get completely discharged across the load and the capacitor C.
This allows the inductor to consistently produce the boost voltage at an efficient rate.
In the discontinuous mode, the transistor switch ON timing may be so wide apart that the inductor may be allowed to get discharged fully and stay inactive in between the switch ON periods of the transistor, creating huge ripple voltages across the load and the capacitor C.
This could make the output less efficient and with more fluctuations.
The best approach is to calculate the ON/OFF time of the transistor which yields maximum stable voltage across the output, meaning we need to make sure that the inductor is optimally switched such that it’s neither switched ON too quickly which might not allow it to discharge optimally, and nor switch it ON very late which might drain it an inefficient point.
Calculating, Inductance, Current, Voltage and Duty Cycle in a Boost Converter
Here we’ll discuss only the continuous mode which is the preferable way to operate a boost converter, let’s evaluate the calculations involved with a boost converter in a continuous mode:
While the transistor is in the switched ON phase, the input source voltage (
) is applied across the inductor, inducing a current (
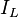) build up through the inductor for a time period, denoted by (t). This may be expressed with the following formula:
) is applied across the inductor, inducing a current (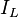) build up through the inductor for a time period, denoted by (t). This may be expressed with the following formula:
ΔIL/Δt = Vt/L
By the time the ON state of the transistor is about to get over, and the transistor is about to switch OFF, the current that is supposed to build up in the inductor may be given by the following formula:
ΔIL(on) = 1/L 0ʃDT
or
Vidt = DT(Vi)/L
Where D is the duty cycle. For understanding its definition you can refer to our previous buck converter related post
L denotes the inductance value of the inductor in Henry.
Now, while the transistor is in the OFF state, and if we assume the diode to be offering minimum voltage drop across it and the capacitor C large enough to be able to produce almost a constant output voltage, then the output current (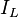) can be deduced with the help of the following expression
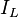) can be deduced with the help of the following expression
Vi - Vo = LdI/dt
Also, the current variations (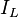) that may occur across the inductor during its discharge period (transistor off state) can be given as:
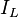) that may occur across the inductor during its discharge period (transistor off state) can be given as:
ΔIL(off) = 1/L x DTʃT (Vi - Vo)dt/L = (Vi - Vo) (1 – D)T / L
Assuming that the converter could be performing with a relatively steady conditions, the magnitude of current or the energy stored inside the inductor throughout the commutation (switching) cycle can be assumed to be steady or at an identical rate, this may be expressed as:
E = ½ L x 2IL
The above also implies that, since the current throughout the commutation period, or at the beginning of the ON state and at the end of the OFF state should be identical, their resultant value of the change in the current level should be a zero, as expressed below:
ΔIL(on) + ΔIL(off) = 0
If we substitute the values of ΔIL(on) and ΔIL(off) in the above formula from the previous derivations, we get:
ΔIL(on) - ΔIL(off) = Vidt/L + (Vi - Vo) (1 – D)T / L = 0
Further simplifying this yields the following result:
Vo/ Vi = 1 / (1 – D)
or
Vo = Vi / (1 – D)
or
Vo = Vi / (1 – D)
The above expression clearly identifies that the output voltage in a boost converter will be always higher than the input supply voltage (across the entire range of the duty cycle, 0 to 1)
Shuffling the terms across the sides in the above equation we get the equation for determining the duty cycle in a boost converter working cycle.
D = 1 – Vo/ Vi
The above evaluations give us the various formulas for determining the different parameters involved in boost converter operations, which can be effectively used for calculating and optimizing an accurate boost converter design.
